ハチの巣は、私にとって40年以上のテーマだ。
「蜂の巣」と検索するといくつか調べたことが出てくる。
たまたまサイエンスZEROを見ていたら、一回り大きい女王バチの幼虫を入れるためにハチは六角形を大きくしなければならない。どうやって大きい六角形を作るのか。
その方法を研究していた人たちが見つけたことは、五角形と七角形を組み合わせることで、より大きな六角形ができるというものだった。
これを知ってしまうと、次は確かめたくなる。
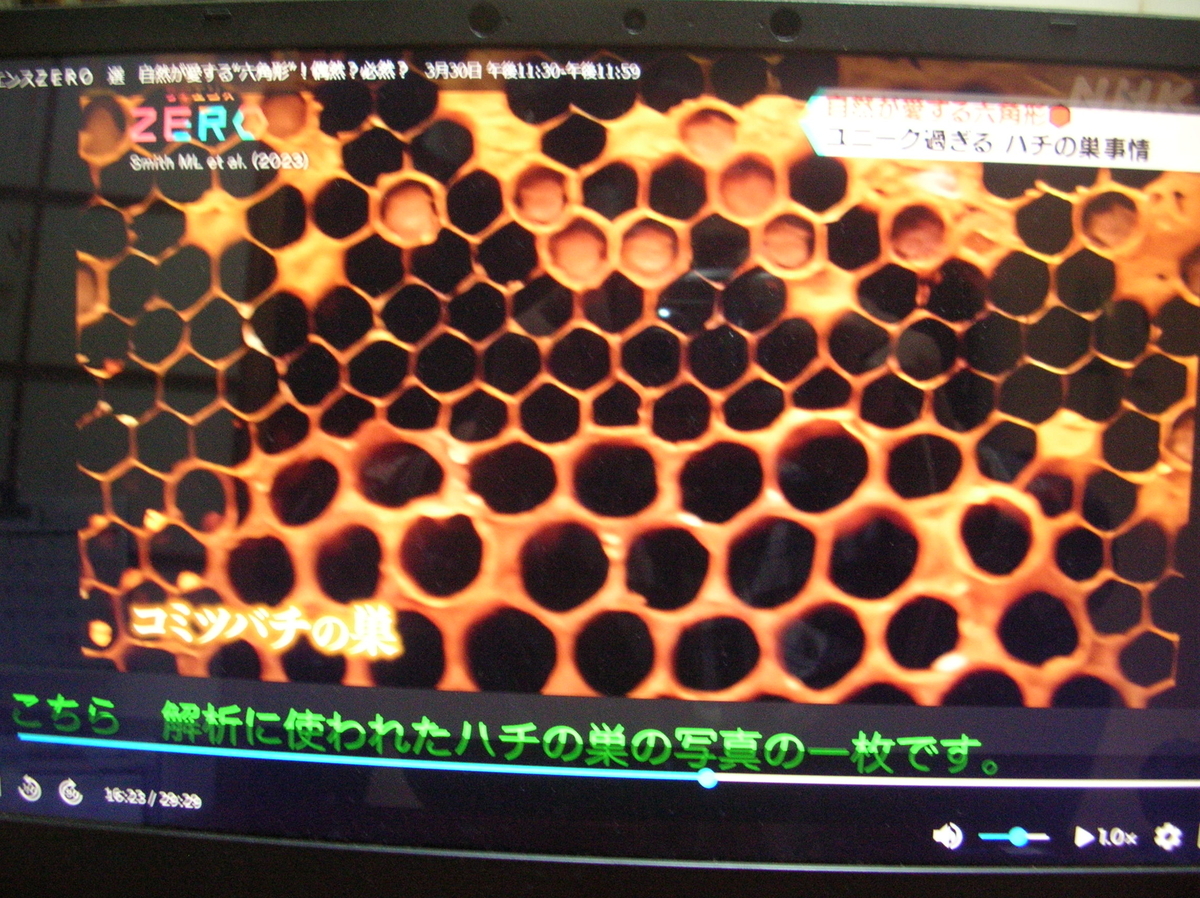
これらの何万枚からの写真から五角形と七角形のペアを見つけ出したという。
面白そうなので、シートを作ることで確かめてみた。
五角形の間の六角形を一つにすると形が崩れる。
五角形の間の六角形を二つおきにすると確かにそうなる。
面白いなあ。
実際にこうやって作ってみると、色々な問いが浮かんでくる。
①いろいろ試したがどうも1.5倍になっているようだ。これが正しいのか。
②これが最も効率の良い作り方だと言っていたけど、どうやって示せばいいのか。
③三つの壁で仕切るということは変えていない。で、七角形をどうやって作るのか。
④これ以外に大きくする方法はないか。
・・・
この問いを確かめるためには、仮説を持たなければならない。
実際にこの図を作る時にいくつかの仮説を設定している。
・ハチにとって壁の分岐を二つにするというのはどうやら基本原理の様だ。
・初めの小さな六角形は同じ大きさで、大きくした後の六角形も同じ大きさになる。
・六角形の一片を減らすと五角形になる。
・五角形の下は七角形でないと次の六角形ができない。つまり七角形は必然。
(3辺+4辺になるから)
・このとき形をくずさず六角形を作るようにすると大きくするしかない。
・大きさ1.5倍は、動かしていると一番ピッタり来るけど、大きい六角形がずれないようにすれば、決まるのではないか。
・七角形が必要だということは、他の多角形にすることで試すことができるのでは。
この仮説通りに数理に基づいて蜂の巣が構成できれば、仮説が正しくハチがそのように行動していることがわかると思う。
ミツバチと社会性カリバチは数学的に同じ方法で巣作り上の難問を解くことを発見
奥が深そうだ。ずっと昔に書いたサイト。
エッシャーの絵 『蜂の巣はなぜ六角形か しきつめの数学 三浦折り 空間を覆う正多面体』 (1991.3)
甘利俊一氏
「自分がやることを知るのが意識なら、やろうとすることを生み出すのが心。
心は必ずしも合理的ではない。」