ここのところ無理をしたせいか身体がえらい。
熱を測ると38.5度。
とりあえず寝ることにした。
フェルマー点とシュタイナー点
昨日は永代経。
朝から花を生けたり、準備をしたりで忙しかった。
ただ、コロナ以前は午前と午後もやっていて、お斎まで用意していたので、
それと比べればずっと楽になった。
が、楽な方へは簡単に流れる。
とてもブログを書く暇がなかった。
だけど、ここ一か月ほどGeoGebraのシートは編集していた。
これはフェルマー点が3点を結ぶ最小のコースだということを、見るだけでわかるようにしたもの。
そして、3点をさらに4点したらどうかという「例の拡張をする」ためのシート。
これを考えた人の名前をとってシュタイナー点という。
だから3点の場合のシュタイナー点はフェルマー点となる。
ずっと以前に作ったものだけど、再度編集し直してみた。
これを見るとシャボン玉ではどう移るのか実験したくなる。
月の出は一日でどれくらい遅くなるか?
菜の花や月は東に日は西に
素敵な蕪村の句だけど、無粋にも「次の日の月の出はどれくらい後なのだろう」と考えてしまう。
計算してみよう。
「月の出は一日でどれくらい遅くなるか?」
まず、ひと月で満月になるわけだから、月の周期は30日。
つまり30日かけて一回転するわけだから、30で割れば一日分が出てくる。
一日は24時間×60分=1440分
これを30で割ると一日分が求まる
1440÷30=48分
つまり、一日で48分遅く出る。
孫:一日=1440分を30日で割ると、どうして月の遅れが求まるの?
爺:いい質問だね。では今度は角度でやってみよう。
月が一か月で地球の周りを一回転するのはいいかな。
孫:ひと月だからね。
爺:30日で360度だから一日360÷30=12度
孫:一日で12度遅く出るんだね。わかった。
爺:これを分に直してみよう。月の動きは太陽とほぼ同じだから、
(24時間×60分)÷360度=4分/度
孫:一度で4分だから12度×4分/度=48分ということか
48分×30日=1440分=24時間つまり一回転する。
八幡公民館のシニアクラブでの法話
八幡公民館のシニアクラブで法話をした。
縁のサロン援助で体操やゲームだけでなく「ためになる話」ということで法話を頼まれることが多くなってきた。
人生の甘いも酸いも経験してきた人たちが、まだ「ためになる話」を聞きたいと思うのか、なぜだろうといろいろ想像してみる。そこで、
「70代の老人はどう生きていくのか」という自分の問題として語ることにしている。
一時間ほどの話だが、たいていは絵や掲示板の言葉を持っていく。
今回は内容については提示資料だけを用意していって、話すことはその場の雰囲気でと考えていた。
用意したが出さない資料もあったけど、何だか自然に離せたような気がする。
「後ろ向きに未来に向かって歩いている」という話は、なかなか納得していただけなかった。⇨【右左前後migihidarizengo.pdf (hamaguri.sakura.ne.jp)】

その場が作りだす関係性
私は一方的に考えていることを語るだけではないし、聞く人たちは私の話を一方的に受け入れるだけではない。その場の関係性がそれぞれの認識を生み出して、語り聞いている。そのことを実感できた会だった。
午後からは高鷲文化財保護協会の理事会。
「虎に翼」が面白くてつい見ている。
きっとこうなるんじゃないかと予想していることが、思わぬ展開を見せるから。
饅頭づくりはまさに回り道の効果!急がばまわれ!
モデルとメタファー
私たちがメタファー(比喩)をするのはわかり易いからだ。
何かにたとえることによって、もっと深く表現できるからだ。
和歌などはこのメタファーを多用している。
だから物事を理解する時にもメタファーを使うと理解が進む。
そしてこのメタファーを突きつめたものがモデル。
理論はモデル化できて応用ができる。
著作権の問題があるけど、この図が一つのモデル。
そして、このモデルはAIのしくみを使った脳のモデル化となっている。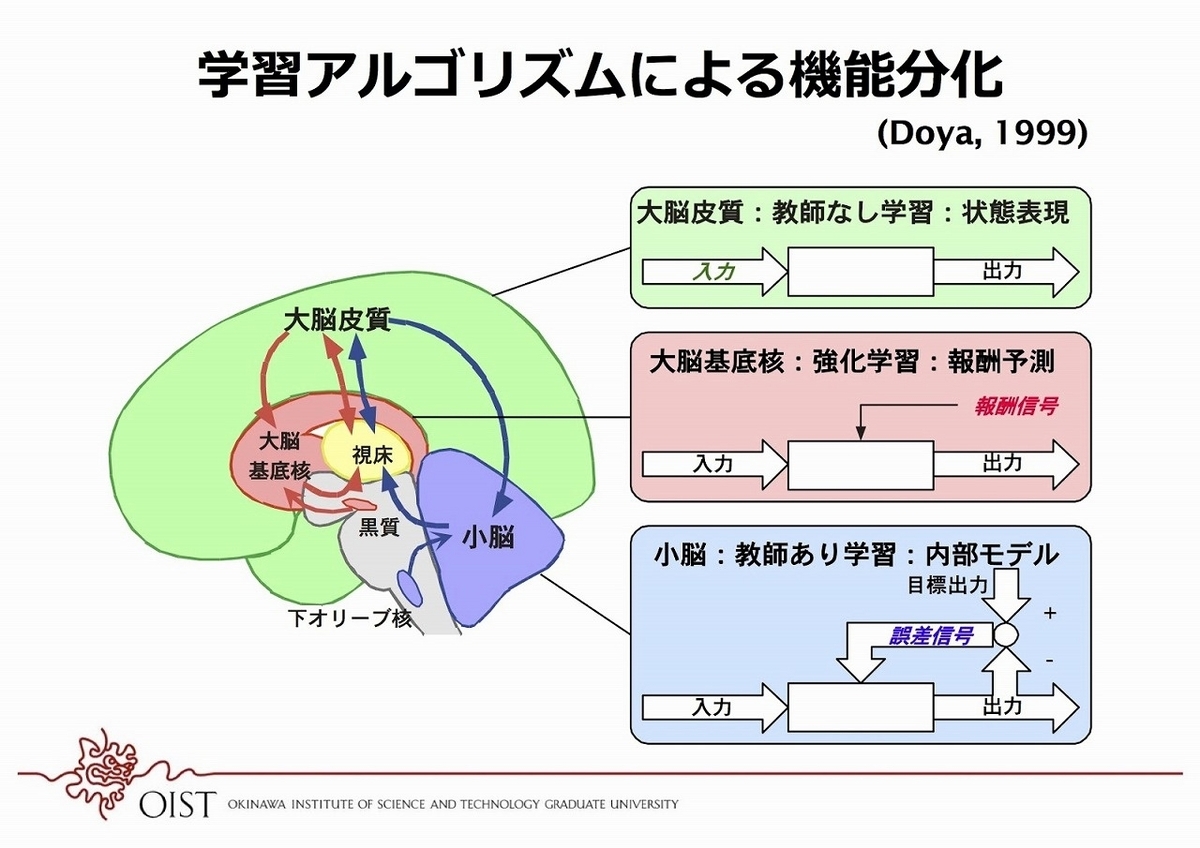
この脳のはたらきは、全て数式にできている。
「教師なし学習」はヘッブ則によって定式化できる。
ヘッブ則とは「同時に発火したニューロン間のシナプス結合は強められる」という現象
⇨【教師なし学習とは?種類・活用事例・クラスタリング手法を簡単解説 】
「教師あり学習」はデルタ則によって定式化できる。
デルタ則とは「答え(正解)と神経の出力差が大きいほど重みの修正値を大きくする」ことで答えにより近くする⇨【ニューラルネットワーク (hamaguri.sakura.ne.jp)】
「強化学習」は報酬信号を出すことによって一定の出力をするように仕向けること。
定型的な出力を決めておくことだと思うけど、そうなる仕組みをAIに組み込むことは案外難しいかもしれない。(強化学習の所をクリックすると説明が出てくる)
あえてメタファーを見つけるとマニュアル通りに実行するようなもの。
モデルベースシステムはこれら3つをさらに組み込んだシステムになる。
さて、モデルは図式化するとよくわかるのはなぜだろうか。
メタファーの良さを表すモデルがあるという。
カテゴリー的距離 ⇨ 面白さ ⤵
比喩の良さ
情緒・感覚的距離 ⇨ わかりやすさ ⤴
これなんか素敵なモデルだと感じる。
さらにコンピュータをメタファーにして認知・学習をモデル化すると
[遺伝]
↓ 形成 学習・発達
[環境] ⇆ 認知・学習システム ⇆ [スキル・知識・価値]
振り返り ⇅ 決定 アクセス
[行動]
となってくるが、これは元となる入出力のブラックボックスモデルを前提にしている。
モデルはモデル化(図化やプログラム化)することによってはじめて使えるモデルとなる。(一方的矢印を⇆に変えてみた。もしかしたら遺伝も⇆かもしれない)





