少し落ち着いてきたが、身体の方がまだ受け付けていない。
いろいろなことを済ますために身体を動かしているだけ。
一人では到底できない。
つれあいのおかげである。
母の病室で書きまくっていたメモをまとめて書き留めておく。
広瀬先生が子どもの答案を見ていたら、その誤答から気がついた。
18-10+5=3 ✖
11ー5-4=10 ✖
広瀬先生は、「答えは本当は二つありうるのでは」と考える。
左から順番に計算すると
18-10+5=8+5=13・・・①
でも、左から順番に計算しないとどうして間違いになるのか。
18-10+5=18-15=3・・・②
11ー5-4=11ー1=10
と子どもが計算してしまうのは、この式に構造的曖昧性があるからではないか。
しかも人間には、
あまりに混沌として複雑すぎる外界の環境に対して主体的に単純化する
傾向があるという。
例えば、①と②のどちらの構造(やり方)を選ぶ方が認知的なコストがより低いのか。
つまり、計算が楽なのは②の方だと感じる。
子どもは、認知コストの低い方を自然に選んでいたということになる。
ここで広瀬先生は、式の( )のはたらきの中に言語との関連に気がつく。
「迷子になった選手の愛犬」と言う言葉と同じ構造を持っていることに。
「(迷子になった選手)の愛犬」か「迷子になった(選手の愛犬)」か、
全く異なるのだ。
そして、この言葉の階層構造と式の階層構造は同じ構造であることに気がつく。
左枝分かれ構造
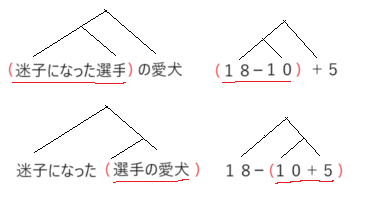
右枝分かれ構造
算数の式と言葉が同じ構造を持つということだ。
例えば、
左枝分かれ構造の式は(迷子になった選手)の愛犬で、
右枝分かれ構造の式は迷子になった(選手の愛犬)だから違うだろ、
計算も同ように違うんだよ、と説明できる。
これはとても面白いし、いろいろな所で応用が利くのではないか。
そのビデオの紹介
「コピペ」から独創へ 括弧の働き
星形正多角形と分数正多角形 国語で代入
1と2では1の方が大きい!?
『西ドイツの小学校で』 (2000.10)