今日は雨だったので家の中の仕事だけ。
いろいろ整理する為に、立ったり歩いたりしてけっこう運動をした。
その合間に以前から気になっていることを考えてみた。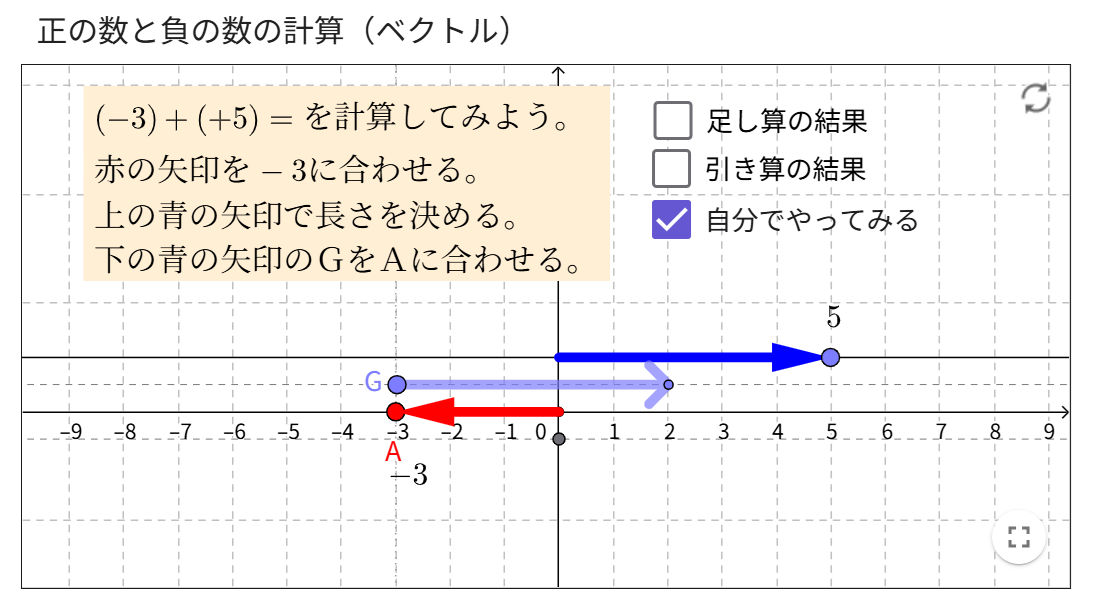
実は、これらのシートを眺めていたら、私自身がわからなくなってきたのだ。
そのわからなさが不思議で、どうしてだろうかと考えたのだ。
なぜわからないのか。
それくらい正・負の数は難しいということか。
最初の混乱は、「ひく」を「後ろにさがる」と演算で考えていたことによる。
符号の-は性質で、演算の-は行動と思い込んでいたのだ。
だから最初にモデルAを考えた。
モデルA
「プラス」=「前を向く」 「マイナス」=「後を向く」
「たす」=「前へ進む」 「ひく」=「後へ進む」
モデルB
「プラス」=「前へ進む」 「マイナス」=「後へ進む」
「たす」=「前を向く」 「ひく」=「後を向く」
ところが、タートルを動かしてみると、どうしてもモデルBになってしまう。
それが最初の混乱。
そして、符号はその後の数値の性質だと思っているから向きにしていた。
でも、-3ー2だと、(ー3)は動かせず、位置ということになってしまう。
これが次の混乱。
そして、「ひく」を演算ととらえているから、「2下る」でぴったりと合ってしまう。
これらが混乱の元だったのだ。
そこで整合性がつくように「プラス」と「たす」を入れ変えてモデルBにしてみた。
「たす」「ひく」は、向きを変えるだけになっている。
そもそも「向きを変える」ことも立派な演算だ。
こちらの方が最初の位置も決まるのでわかり易い。
というわけで、サイトの方もBモデルに全て書き直した。
このように合わないモデルは自在に変えることができる。
ところで、こんなことに時間を掛けてしまったと思わぬでもない。
自分の価値観や欲求に従って行動していただけだが。
でも、このことが同じように混乱している誰かの役に立つのなら幸せを感じる。