地球の公転と日照時間 - 文ちゃんのページ

心が落ち着かないので、何か作ろうと考えた。
久しぶりにGeoGebraで作ってみよう。
そういえば、冬至を過ぎても日没（日の入り）が早くなるのは何故だろうか。

それは、冬至の方が近日点に近く冬至を過ぎても南中時間が遅くなるから。

日の出入りと南中/南中時刻は変化する

近日点の方が地球は速く動くので、自転の時間に対してより進む。
だから、南中時間が遅れる。
南中時間も表現したかったけど、難しすぎるので止めた。
日照時間の数式については、AIに相談したら次の数式を出したので、それを使い、さらに合うように少し変形した。

基本公式（標準形）

$\boxed{ T = \frac{2}{15} \cos^{-1}(-\tan\phi \tan\delta) \quad (\text{時間}) }$

記号の意味

$T$ ：日中の長さ（時間）
$\phi$ ：観測地点の緯度
$\delta$ ：太陽の赤緯（季節で変化）
$15$ ：地球の自転
（ $360^\circ ÷ 24\text{h} = 15^\circ/\text{h}$ ）

どうやって出したのかはわからないが、確かめると少し違うだけ。

次のシートの地球の位置は自由に動かすことができる。北緯も変えられる。

ところで、地球は太陽の周りを一年かけて回るのだから、３６０度÷３６５日で、
一日に角度で約１度回転する。
つまり、２４時間で１度だから、これを分に直すと、一日２４時間×６０分。
これを３６０度で割ると、４分ぶんだけ余分に回転しているということがわかる。
絶対位置に関しては２４時間ではなく、４分引いた時間で一回転するということだ。
上の図の一日分は１°で、自転でいうと４分だということ。
つまり、
地球は一日２４時間にするために４分ずつ余分に回転しなければならないのだ。

なぜ冬至で日照時間が最小になるのかは、地軸の傾きによる。
この角度が太陽に対して最大になる位置が冬至で、たまたまこの場所。
次のシートで、北半球では春夏秋冬がどこだかわかってくる。

近日点で早くなるのは楕円軌道だから。楕円軌道についての図。

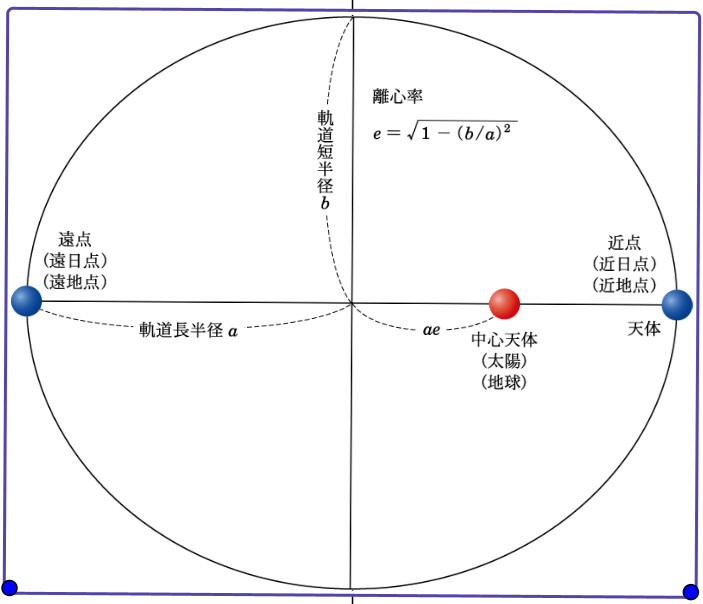
楕円だと近日点で早くなるのはケプラーが見つけた。

次のシートは最初の緯度を北緯３５°としてシュミレーションした。
緯度を変化させると仕組みが何となくわかってくる。

太陽の見かけの円が、地平線上にある時が日照時間。
これなら日照時間を計算で出せることが予想できる。
これは昔作ったけど、今見るとこれを理解すること自体が難しいな。
でも、こうやっていくつかのシートを並べるとイメージが膨らむような気がする。

その他の 天体シュミレーション

病院へ行ったら、手術を進められた。
予約をお願いしてきた。

この日照時間の計算式はどうやって求めたの？

とても本質的な質問です。

この式は **「地球を球として、天球上の幾何」**から 一直線に導かれます。
順にほどいていきますね。

出発点（考え方の芯）

日照時間＝
太陽が地平線の上にある間に、地球が回転した角度

つまり
👉 角度の問題です。

① 天球で考える（図形の舞台）

地球中心を原点とする天球を考えます。

地平線：天球を切る平面
太陽：赤緯 $\delta$ の位置を回る点
観測者：緯度 $\phi$

太陽は
👉 赤緯 $\delta$ の小円
を 24 時間で1周します。

② 日の出・日の入りの条件

日の出・日の入りでは：

太陽高度 h = 0^{\circ}

天球の基本公式（球面三角）：

\sin h = \sin\phi \sin\delta + \cos\phi \cos\delta \cos H

ここで

$H$ ：時角（南中からの角度）

日の出・日の入りでは $h=0$ ：

0 = \sin ϕ \sin δ + \cos ϕ \cos δ \cos H

③ 時角 $H$ を解く

整理すると：

\cos H = - \tan ϕ \tan δ

ここで

$H_0$ ：日の出（または日の入り）時の時角

H_{0} = \cos^{- 1} (- \tan ϕ \tan δ)

④ 日照時間は「この2倍」

太陽は

$-H_0$ → $+H_0$

の間、地平線の上にあります。

よって角度は

2 H_{0​}

⑤ 角度 → 時間に変換

地球は

$360^\circ$ を 24 時間で回転
$15^{\circ} = 1時間したがって$

T = \frac{2H_0}{15}

これに③を代入：

\boxed{ T = \frac{2}{15} \cos^{-1}(-\tan\phi \tan\delta) }