30年ほど前に、生徒が発見した定理と出会った。
16、米倉の定理・・・生徒が発見した定理 田尻の定理 上村の定理 (1991.3)
直角三角形の頂点を外心に折り曲げると、相似三角形ができるという。
びっくりした。
ここから様々な実践が始まった記念すべき定理である。
ここから拡張する数学という方法に開眼した。
でも、この外心の意味がはっきりとはしなかった。
外心を中心に回転させれば、相似三角形ができることも生徒が発見した。
でも、外心以外を試そうとは思わなかった。
今回、等力点やフェルマー点を作図していて、ついに結びついた。
まとめると、
①米倉の定理と外心
②「外心と相似」で拡張する方法
③外心が中心だけど、外心でなくても相似になる点がある(三円交点)
➃外接三角形もできる
⑤等力点、フェルマー点を中心にすれば、正三角形になる
⑥内心を中心にすれば内接三角形も外接三角形も相似
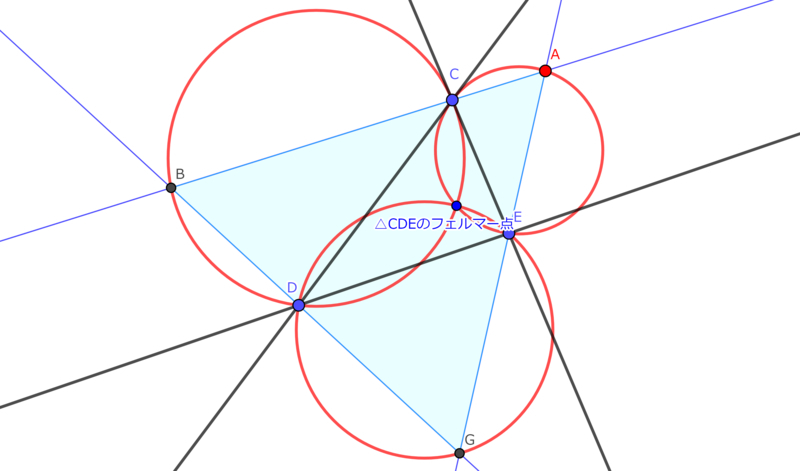
意味の世界は、無限に広まっていると思う。
そのほんの少しを垣間見て、また混沌の世界に舞い戻る。
でも、そういう世界がまだ無限にひろがっていると思うと、
その一端に触れられた幸せを感じることができる。