ニューラルネットワークはどんな働きをしているのか。
Rのパッケージnnet(ニューラルネットワーク)にいろいろな値を入力して、どんな出力がされるか確かめてみた。
入力データはサイン関数で10個。下のグラフのデータを入力する。
input output
1 0.025 0.4530697
2 0.125 0.2878680
3 0.200 0.2146830
4 0.300 0.2146830
5 0.400 0.3236644
6 0.475 0.4530697
7 0.550 0.5927051
8 0.650 0.7427051
9 0.800 0.7853170
10 0.975 0.5469303
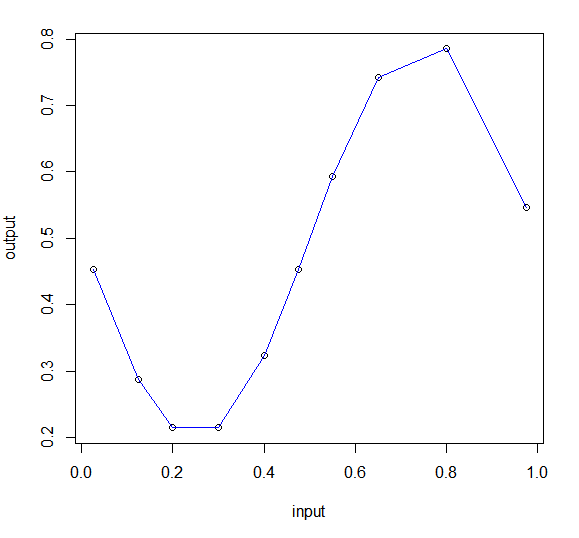
かなりばらつきがあるけど、このデータからサイン関数が再現出来たらすごい。
実行したスクリプトを書いておくと
―――――――――――――――――――――――――――
#バックプロパゲーションによる学習
library(nnet)
train <- read.csv("sin9.csv",h=T)
train
plot(train)
valid <- read.csv("sin2.csv",h=T)
valid
plot(valid)
#nnetのhelpより size:中間層、maxit:くりかえし回数
#size number of units in the hidden layer. Can be zero if there are skip-layer units.
#それから,predの"type"で出力形式を指定します.通常は"class"でよい
#predic.nnetのhelpより
#If type = "raw", the matrix of values returned by the trained network; if type = "class", the corresponding class
#(which is probably only useful if the net was generated by nnet.formula).
sin1 <- nnet(data=train,output~input,size=3,maxit=2000);
# weights: 10
yosoku1 <- predict(sin1,valid,type="raw")
plot(valid,type="b")
points(train,type="b",col=2,pch=16)
points(valid$input,yosoku1,type="b",col=4,pch=20)
lines(valid$input,yosoku1,col=4)
―――――――――――――――――――――――――――
赤い字がニューラルネットワークのパッケージ。
バックプロパゲーションによってsin1というBBができる。
そこにxを入力してyを出したのがyosoku1。
これで結果を出してみると次の結果になる。
白丸がサインの正しい値。赤いデータ(入力値)から青いデータ(nnetからできたsin1)を予測したのだ。
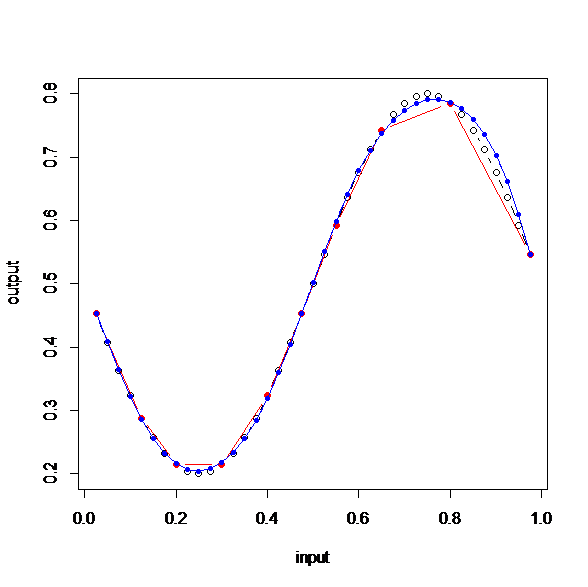
右の上が少しずれているけど、かなり近い。
これはすごいと思う。中間層は3で重みを計算する回数は2000回。
さらに、中間層(size)を10にしてみる。
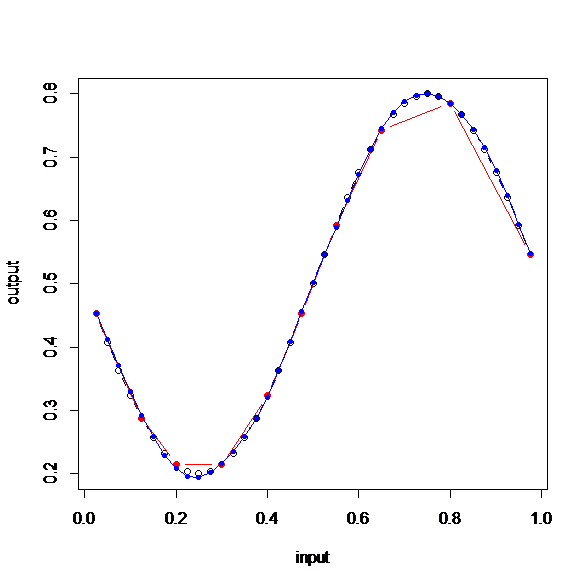
もうほとんどサイン関数だ。
たった10個のデータを与えただけで、サイン関数が再現できたということだ。
これはすごい。
ニューラルネットワーク恐るべし。