先日のわしょう会で、岐阜大学の田中先生から「結び目の数学」の話を聞いた。
テーマは、高校生に対して行ったセミナーの「結び目の理論」の導入の話。
以前からいつかやろうと思っていたので、ちょうど良い機会だった。
聞いていて、ほとんど理解できなかったが、考える方向性はわかった。
最初に、結び目がほどけるのかほどけないのかと問う。
具体的な結び目を提示して、より簡単になるように結び目の交点を移動させて、より簡単な図形にする。
そうすると、ほどけるのかほどけないかがわかる。
では、それをどのように表現するのか。
つまり数値(不変量)として表すにはどうしたらいいのか。
実践では、不変量を最初に与えてそれを使って確認するという流れだったが、
私は、例によって、不変量そのものを作りだすことの方が面白いと思って、その流れを考えてみた。
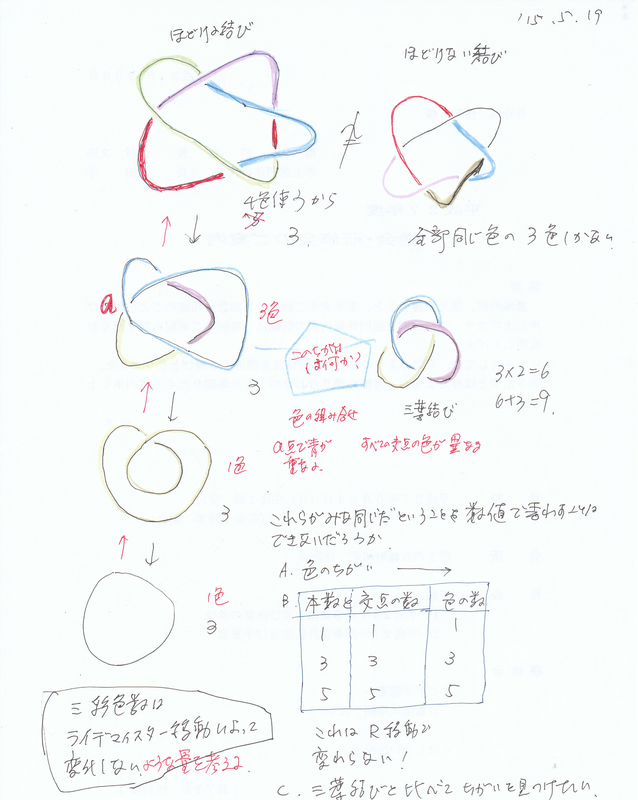
左の結び目はほどけるものであり、右側のものはほどけない。
この違いを数値で表すにはどうしたらいいのか。
まず、左側を上に変形しても変わらないものを見つける。
例えば、交点の数と線の本数の関係は変わらないが、それはほどけない場合も同じでダメ。
次に線に色を塗ったとき、交点に三色集まるのかどうかが大きな違いになる。
例えば、a点では2色になるが、三色になる場合がほどけない場合となる。
ここから、三彩色数を見つけていく。
ポイントは、三色を使って色分けしたときに、ほどける結び目は必ず3色にはならないということで、
そこから、組み合わせの数を不変量とするアイディアが生まれる。
次は、3色を拡張する方向。
そして、その他に不変量が無いかどうか。
つまり、結び目を完全に分類できる不変量を見つけることが目標となり、とてもわかりやすい。
だから、中学生にも十分に取り組むことができる。
そして、結び目の数学は、予備知識が少なく、すぐに最先端(完全な不変量を求めることはまだ未解決)に達することができる。