小さい人たちに教えていた時、「水平線は直線でないとおかしい」と言ったことがある。もし曲がっているとしたら、後ろの方は落ち込んでいるからだ。(つい先日までそう思っていた)それ以来、水平線を見るたびに直線かどうか確認をした。
例えばこの写真の地球は円でしょうか?
何と円ではありません!。
何と円ではありません!。

海抜0mだと水平線は直線。
ところが、高度1万mぐらいになると、曲がっているように見える。
そもそも、宇宙ステーションから地球を見ると円に見える。
どこから円でどこから直線になるんだ。
円から直線に急になるはずがないと気がついた。
ところが、高度1万mぐらいになると、曲がっているように見える。
そもそも、宇宙ステーションから地球を見ると円に見える。
どこから円でどこから直線になるんだ。
円から直線に急になるはずがないと気がついた。
そのことを、高度1万mで考え出し、結論が出たのは海抜200mの地点。
時間は2週間弱かかってしまった。
時間は2週間弱かかってしまった。
最初、数式で表そうと考えていろいろ計算していた。
考えているうちに、簡単な方法が見つかり、計算しなくてもわかることに気がついた。その方法とは、円錐曲線の切断。
考えているうちに、簡単な方法が見つかり、計算しなくてもわかることに気がついた。その方法とは、円錐曲線の切断。
そして、結論は、「水平線は双曲線である!」ということだ。
少し理論的な話
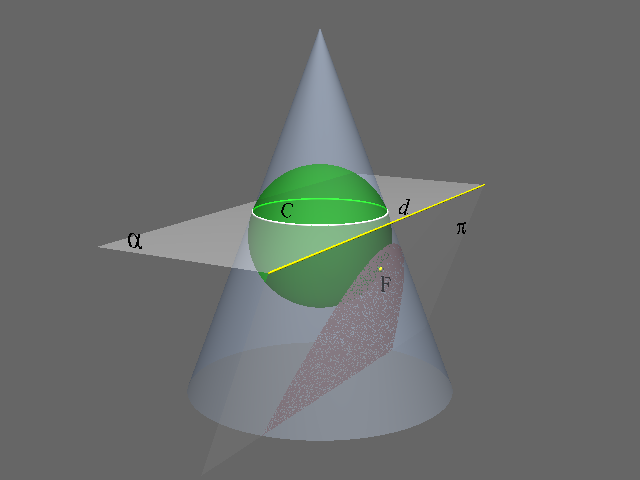
まず、この図で、緑の球を地球としよう。
普通、円錐を平面で切断してできる円錐曲線は、下図のように、円→楕円→放物線→双曲線と変化する。
この場合、私たちの視点は円錐の頂点にある。
地球の3600km上空から地球を見ると地球は円に見えることはわかる。(ひまわりの写真)
もし、地球が円盤だったら角度によって楕円(緑)に見えるが、球なので必ず円(ピンク)に見える。

ここで、円錐の頂点をだんだん下げていく(高度を下げるとだんだん平たい円錐になる)。
高度を下げても、地球は円に見えることは変わらない。
ところが、もっと下げると、円全体が視界に入らなくなってきて、部分しか見えなくなる。
さて、この時、その円孤はどう見えるのかということだ。
上図でいうと、ピンクの地球は、どう見えるのかということになる。
最初、それは円の一部であり、頂点から見ても距離が等しいので円としか考えられなかった。
実はここが一番わからなかったことろで、見方が変わったのは、何を見ているのかに意識がいったからだ。
私たちが見るということは、その影を平面に投影し、その平面の影を見ているということだ。
つまり、この円の影を平面に写した場合にそれがどんな影になるのか。
その影は、前の図でπの平面で切断したのと同じことになる。
私たちが水平線を見るということは、円錐の底面と垂直な平面で切断したときの切断面を見ると同じである。
そして、その切断面は上図のように双曲線(橙)となる。(反比例のグラフ。もし母線と平行なら放物線)
これは意外な結果なのだが、私たちが水平線を見る所は、必ず高さがあるので双曲線となる。
そして、その双曲線の曲がり具合は高さによる。
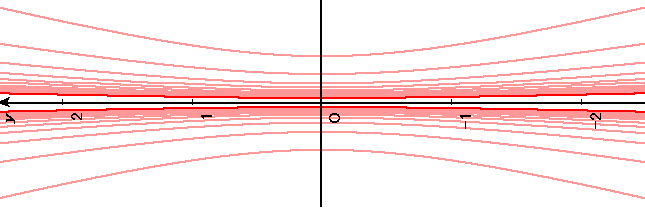
グラフにしてみた。
真ん中の黒い線が水平線。
(海の水平線は、本当の水平線よりも必ず下にあるはずで、計算してみた。富士山でなんと2度以上も下。)
そして、ピンクの線が双曲線。(実際に見える水平線)
高くなるにしたがって、下の方の双曲線になる。(上の線は本当の水平線よりも地下に潜った場合)
高度を上げるにしたがって、この双曲線はやがて放物線になり、楕円となって、全体が視野に入ると円となる。
そうすると、
「だんだん下がるということは、後ろはどうなるの? 落ち込んでいるの?」
と疑問が浮かぶ。
でも、だんだん右に視点を移すと、写すキャンパスも移動するので、やはり同じように見えるのである。
(これは写すキャンバスを円筒にすると同じことだが、私たちが一点を見る場合は平面であり、
写真に撮った場合と同じで平面に映すので、双曲線になる。水平線の写真で確かめた。)
立体シュミレーション↓
このことについてはこのサイトを参考。
なお、直線に見えて、双曲線に見えないのは、曲率が小さいのと、視点をずらしていった時に同じように見えるためである。
そして、この平面での地球の影は、
右にも左にも無限に延長される漸近線(直線=円錐の母線)にどんどん近づいていく。
なお、このことは、懐中電灯で簡単に確かめることができる。
水平線が直線であると思い込んできた私には、結果を受け容れるのにかなり時間がかかってしまった。